Representación del sonido
The study of sound has given rise to various models, each with a particular focus.
Formas de representación del sonido
Representación temporal
Esta representación muestra la evolución de la intensidad de la señal de sonido en el tiempo.
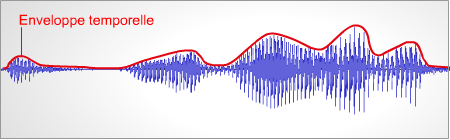
La parte en azul muestra la evolución de la intensidad de un sonido de voz en el tiempo. Esta visión temporal permite, sobre todo, constatar la evolución de la envolvente temporal (línea roja), que, por ejemplo, desempeña un papel importante en la percepción del habla.
Representación de frecuencias (o espectral)
Este modo permite visualizar la composición frecuencial de un sonido, pero también la intensidad de cada frecuencia.
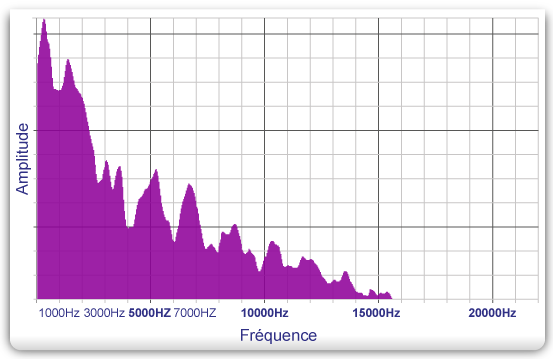
En esta gráfica, se puede apreciar la composición espectral de la muestra sonora precedente. En este ejemplo se constata que las frecuencias del sonido seleccionado se oyen entre 80 Hz y 15.500 Hz
Representación tridimensional: el sonograma o espectrograma
Se trata de realizar la representación tiempo-frecuencia del sonido. Se dibuja la distribución de energía del sonido en función del tiempo y de las frecuencias. El monograma se utiliza mucho para analizar la señal de voz.
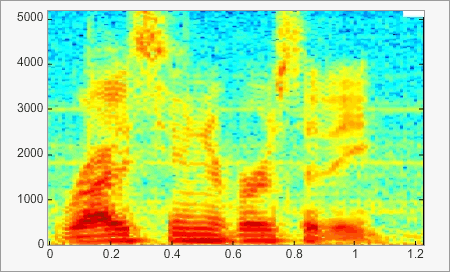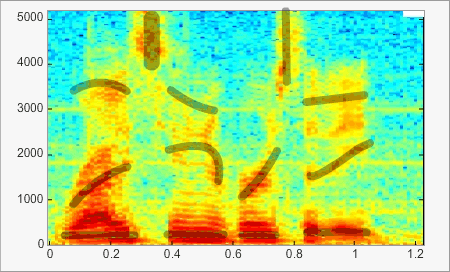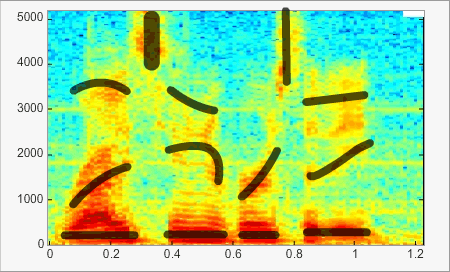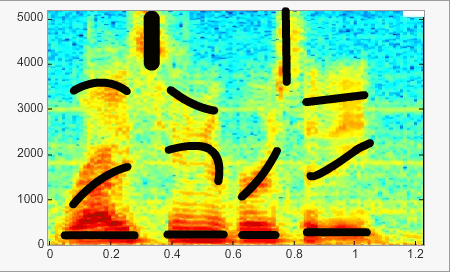
El siguiente ejemplo demuestra la evolución de la frecuencia y de la intensidad en el tiempo. La intensidad se define por el color: en mayor cuanto más se aproxima al rojo. En este ejemplo se distinguen bien las formantes formantes de las vocales, las formantes transitorias, etc. Mueva el ratón sobre la imagen para resaltar (líneas negras) los movimientos que tienen un papel importante en la percepción del habla (véase también el capítulo «palabra»).
Algunos sonidos comunes
Palabra

Spectrum of the French spoken word « cochlée ». The energy content will vary for each syllable. Each vowel will have three or four peaks of energy, called formant, located at specific frequencies.
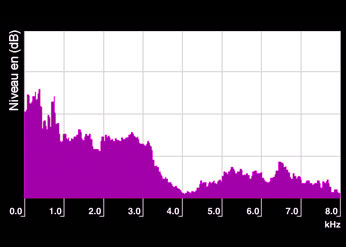
Ruido blanco

Espectro teórico de un ruido blanco que ha sido limitado a la banda de frecuencia 500-6500 Hz. En el ruido blanco, al ser continuo y estar formado por una banda continua de frecuencias, no es posible individualizar líneas espectrales concretas.
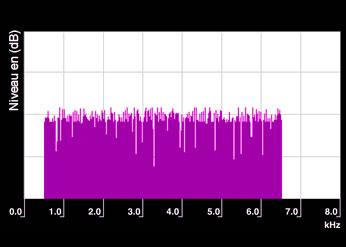
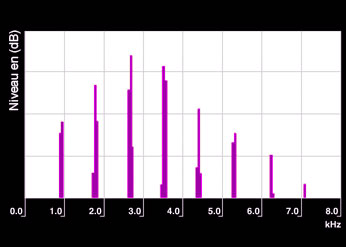
Música

Espectro real de un sonido musical que comprende un fundamental de 880 Hz (nota la 4) y 7 armónicos, cuyas frecuencias son los múltiplos enteros de la frecuencia fundamental. Como para el tono puro, las líneas espectrales son más largas de lo que prevee la teoría.
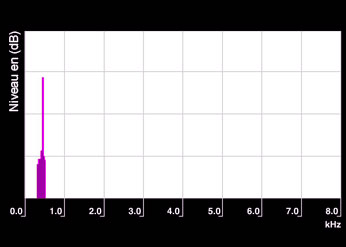
Tono puro

Espectro real de un tono puro de 440 Hz de frecuencia obtenido con analizador de espectro. La línea espectral real es siempre más ancha que lo que prevee la teoría.
Escala de los Belios
La intensidad más baja que percibe el oído humano, en promedio, es de 10-12 W.m-2 y la más alta alrededor de 1 10-12 W.m-2. Entre ambas medidas existe una relación de un billón y como esta escala no es fácil de usar se transcribió a belios. Los belios están basados sobre un sistema logarítmico de evaluación relativa, es decir en la relación entre dos cantidades de la misma especie.
Por ejemplo, para evaluar el nivel de intensidad de sonido, el valor de referencia será la menor intensidad a la que el oído humano sea sensible (antes indicado como: I = 10-12 W.m-2). Si se quiere conocer a qué nivel corresponde I1 = 1 W.m-2, basta con obtener el logaritmo de relación entre I1 e I .
Nivel de intensidad = log10 (I1/I ) = log10 (1012) = 12 belios.
LI = 10 x log10(I1/I ). If the acoustic intensity is doubled, the sound level is multiplied by 2 (an increase of +3 dB).
Añadiendo un factor multiplicador de 10, se obtiene una escala expresada en decibelios (dB) que corresponde a la de la sonoridad (sensación subjetive de intensidad sonora). Así, una intensidad de 1 W.m-2 corresponde a un nivel de intensidad acústica de 120 decibelios.
LI = 10.log10 (I1/I ). Si la intensidad acústica se duplica, el nivel sonoro se multiplica por 2 (I que equivales a un incremento de 3 dB)
Cuando se evalúa el nivel de presión acústica, la unidad del decibel puede ser seguida por las letras SPL («Nivel de presión de sonido») que caracterizan a la presión acústica de referencia p0 = 20 * 10-6 Pa = 20 mPa (presión acústica mínima a la que es sensible el oído humano).
Como se ha mencionado anteriormente, la intensidad acústica es proporcional a la presión acústica p al cuadrado. Por tanto, el nivel de presión acústica se define por la siguiente ecuación: LSPL 20.log10 = (p/p0). Si la presión acústica p se duplica, la intensidad sonora se multiplica por 4 (lo que equivale a un incremento de +6 dB).
Los umbrales de audición se expresan en decibelios de pérdida, dB HL (“Hearing Loss” = pérdida de audición). Esta escala tiene en cuenta las diferentes sensibilidades del oído en función de las frecuencias. Por ejemplo, una persona con audición normal detecta el sonido de 500Hz a partir de los 10 dB SPL, un sonido de 2000Hz a partir de 0dB SPL y un sonido de 8000Hz sonido a partir de los 20 dB SPL. Para la aplicación en Audiología de estos hechos, los umbrales de audición normal a las diferentes frecuencias se llevan a 0dB HL. Por lo tanto, el audiograma permite representar los umbrales de audición en relación con una referencia establecida en el estudio de una amplia población normooyente. De esta forma, se pueden clasificar los diferentes grados de sordera gracias a esta escala (ver el apartado de audiometría tonal).